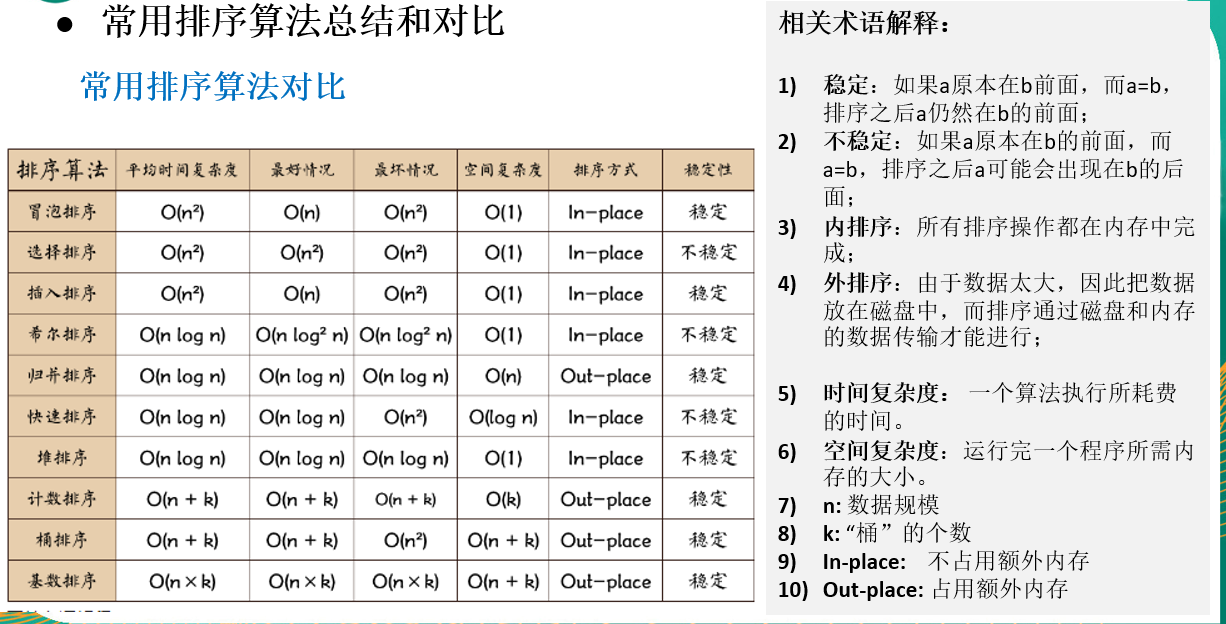
排序算法
排序算法
排序
1.内部排序 将需要处理的所有数据都加载到内部存储器中进行排序 2.外部排序法 数据量过大,无法全部加载到内存
内部排序
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 简单排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 技术排序
冒泡排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[] arr= new int[]{2,5,8,0};
int temp =0;
int count = arr.length-1;
for (int j=1;j<=count;j++) {
for (int i = 0; i < arr.length - j; i++) {
if (arr[i] > arr[i + 1]) {
temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
}
for (var val:arr ) {
System.out.println(val);
}
进行优化,如果排序已经在完成,则不在继续
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int[] arr= new int[]{2,5,8,0};
int temp =0;
int count = arr.length-1;
boolean flag=false;
for (int j=1;j<=count;j++) {
//优化 某一次已经完成排序了,则不在进行排序
flag=false;
for (int i = 0; i < arr.length - j; i++) {
if (arr[i] > arr[i + 1]) {
flag=true;
temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
if(!flag){
break;
}
}
for (var val:arr ) {
System.out.println(val);
}
选择排序
第一次从 arr[0]-arr[n-1]选取最小值与 arr[0]交换,第二次从 arr[1]-arr[n-1]选取最小值和 arr[1]交换,通过 n-1 次,获取到有序的队列
1
2
3
4
5
6
7
8
9
10
11
12
13
for(int i=0;i<arr.length;i++)
{
for(int j=i;j<arr.length;j++)
{
if(arr[i]>arr[j])
{
int temp =arr[i];
arr[i] = arr[j];
arr[j]=temp;
}
}
}
插入排序
把 n 个带排序元素看成一个有序表和无需表,开始有序表只有一个元素,无序表包含 n-1 个元素,排序过程中每次去无序表中取一个元素,向有序表中寻找合适位置插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//插入排序实现
public static void Sort(int[] arr)
{
int val =0;
//记录插入的位置
boolean flag =false;
int index =0;
//外层遍历有序列表
for(int i=1;i<arr.length;i++)
{
val =arr[i];
//初始插入位置
index=i-1;
//内层遍历有序列表,寻找插入位置
while (index>=0&&val>arr[index])
{
arr[index+1]=arr[index];
index--;
}
arr[index+1]=val;
}
}
希尔排序 缩小增量排序
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序,随着增量逐渐减少,每组包含的关键词越来越多,当增量减至 1 时,整个文件恰被分成一组,算法便终止,希尔排序对直接插入进行了优化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//移位法
public static void InsertSort2(int[] arr)
{
for(int gap=arr.length/2;gap>0;gap/=2)
{
for(int i=gap;i<arr.length;i++)
{
int index = i;
int val = arr[i];
// if(arr[i]<arr[index-gap]) {
while (index - gap >= 0 && val < arr[index-gap]) {
arr[index] = arr[index - gap];
index -= gap;
}
//}
arr[index]=val;
// for(int j=i-gap;j>=0;j-=gap)
// {
// if(arr[j]>arr[j+gap])
// {
// temp=arr[j];
// arr[j]=arr[gap+j];
// arr[gap+j]=temp;
// }
// }
}
}
}
快速排序
快速排序是对冒泡排序的改进,采用分治的思想
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//快速排序
public void QuickSort(int[] arr)
{
QuickSort(arr,0,arr.length-1);
}
//快速排序
public void QuickSort(int[] arr,int left,int right)
{
int pivot = partion(arr,left,right);
if(left<right) {
QuickSort(arr, left, pivot - 1);
QuickSort(arr, pivot + 1, right);
}
}
public int partion(int arr[],int left,int right)
{
int key =arr[left];
while(left<right) {
while (left < right && arr[right] >= key) {
right--;
}
arr[left] = arr[right];
while (left < right && arr[left] <= key) {
left++;
}
arr[right]=arr[left];
}
arr[left]=key;
return left;
}
排序速度
堆排序
堆:是具有以下性质的完全二叉树,每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆,反之则是小顶堆。 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(nlogn),它也是不稳定排序,一般升序采用大顶堆,降序采用小顶堆 堆排序思想:将待排序的序列构造成一个大顶堆,此时整个序列的最大值就是堆顶的根节点,将它与堆数组的末尾元素进行交换,此时末尾元素就是最大值,然后将剩余的 n-1 个序列重新构造成一个堆,这样就会得到 n 个元素中的次大值,如此反复就能得到一个有序序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
//编写一个堆排序的方法
public static void heapSort(int arr[]) {
int temp = 0;
System.out.println("堆排序!!");
// //分步完成
// adjustHeap(arr, 1, arr.length);
// System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
//
// adjustHeap(arr, 0, arr.length);
// System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4
//完成我们最终代码
//将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
for(int i = arr.length / 2 -1; i >=0; i--) {
adjustHeap(arr, i, arr.length);
}
/*
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
*/
for(int j = arr.length-1;j >0; j--) {
//交换
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
//System.out.println("数组=" + Arrays.toString(arr));
}
//将一个数组(二叉树), 调整成一个大顶堆
/**
* 功能: 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
* 举例 int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
* 如果我们再次调用 adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param lenght 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int arr[], int i, int lenght) {
int temp = arr[i];//先取出当前元素的值,保存在临时变量
//开始调整
//说明
//1. k = i * 2 + 1 k 是 i结点的左子结点
for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
k++; // k 指向右子结点
}
if(arr[k] > temp) { //如果子结点大于父结点
arr[i] = arr[k]; //把较大的值赋给当前结点
i = k; //!!! i 指向 k,继续循环比较
} else {
break;//!
}
}
//当for 循环结束后,我们已经将以i 为父结点的树的最大值,放在了 最顶(局部)
arr[i] = temp;//将temp值放到调整后的位置
}
}
本文由作者按照 CC BY 4.0 进行授权